优化｜随机零阶优化算法分析_耀世-耀世娱乐网络科技媒体工作室

Title
优化｜随机零阶优化算法分析

发布时间：2024-07-01 15:24:41 作者：佚名点击量：

原文：Random Gradient-Free Minimization of Convex Functions. Found Comput Math 17, 527–566 (2017). https://doi.org/10.1007/s10208-015-9296-2

原文作者：Yurii Nesterov, Vladimir Spokoiny 论文解读者：陈宇文

本次知识分享活动挑选Yurii Nesterov与Vladimir Spokoiny发表的Random Gradient-Free Minimization of Convex Functions论文，带领大家梳理论文中的无梯度优化算法的核心思想以及与传统方法之间的联系。

最近几年，零阶算法因为其需要的获取信息条件的宽松而受到关注。相比于一阶或者更高阶的算法，零阶算法只需要获取函数值本身，因此很适用于黑盒优化的问题。本文中，我们将梳理Nesterov的论文中提到的一种零阶算法，总结这一类零阶算法有用的性质和结论。

优化算法中我们会根据可以能够获取的信息定义算法的阶数，常见的有一阶算法(梯度下降)和二阶算法(内点法，半光滑牛顿法)，甚至更高阶算法(cubic regularization)。那如果我们连最常见的一阶梯度信息都缺失呢？我们还可以利用函数值进行优化，例如许多智能算法和有限差分的方法。相较于前者，后者往往能得到较好的理论结果。但是简单的有限差分需要对变量每一个维度进行扰动，计算一次近似梯度需要 $O(n)$ 个不同的函数值。在文[1]中，Nesterov分析了一种特殊的零阶算法，每一次梯度近似只需要 $O(1)$ 个不同的函数值：

$x_{k+1}=x_k ? h_k \\cdot \\frac{f(x_k + \\mu_k u)? f (x_k)}{\\mu_k}\\cdot u. \\qquad \\qquad (1) \\\\$

同时文[1]中总结了许多有趣的理论，我们将对它们一一展开。

对于算法（1），如果我们选取 $\\mu_k \ o 0$ ，那么取极限下的算法可以理解为 $x_k$ 沿着方向梯度 $u$ 的方向下降，如下所示：

$x_{k+1}=x_k ? h_k f'(x_k , u)u. \\\\$

如果我们定义 $g_0(x,u) :=f'(x, u)u$ ，那么算法则可写成

$x_{k+1}=x_k ? h_k g_0(x,u) \\qquad \\qquad (2) \\\\$

此时我们对方向 $u$ 没有任何假设，它可以是任何方向。那我们应该如何选取这个方向向量 $u$ 呢？

如果采用random search方法的思想[2]：假设方向 $u$ 的采样满足多维高斯分布(协方差矩阵取单位矩阵)，那么当我们对 $u$ 求取函数 $f (x + \\mu u)$ 期望可以得到

$f_{\\mu}(x) :=\\mathbb{E}_u( f (x + \\mu u)). \\\\$

$f_{\\mu}(x)$ 的梯度可以写成

$\ abla f_{\\mu}(x)=\\frac{1}{\\mu}\\mathbb{E}_u( f (x + \\mu u)u)=\\frac{1}{\\mu}\\mathbb{E}_u([f (x + \\mu u) - f(x)]u), \\\\$

其中最后一个等式中加入 $f(x)$ 项可以根据高斯分布的对称性得到。如果我们对 $\ abla f_{\\mu}(x)$ 进行采样，那么我们得到采样后的梯度 $g_{\\mu}(x)$

$g_{\\mu}(x,u) :=\\frac{f(x+\\mu u)? f (x) }{\\mu}\\cdot u. \\\\$

这时，我们可以发现算法（1）可以重新写成

$x_{k+1}=x_k ? h_k \\cdot \ extcolor{red}{g_{\\mu}(x_k,u)}. \\qquad \\qquad \\\\$

所以算法（1）可以看成对 $f$ 的近似函数 $f_{\\mu}$ 的随机梯度下降。也是从随机算法的角度出发，文[1]分析了许多 $f_{\\mu}(x)$ 和 $f(x)$ 在不同阶数泰勒展开下的误差，同时通过 $f_\\mu$ 这个中介进一步分析算法（1）的收敛性。

我们回顾 $f_{\\mu}(x)$ 的定义：

$f_{\\mu}(x) :=\\mathbb{E}_u( f (x + \\mu u))=\\frac{1}{\\kappa}\\int_{E}f(x + \\mu u) e^{-\\frac{1}{2}\\|u\\|^2}du. \\\\$

我们称函数 $f_{\\mu}(x)$ 是 $f(x)$ 的高斯光滑近似。同时，它还具有如下一些特性：

那么函数 $f_{\\mu}(x)$ 和 $f(x)$ 存在哪些关系呢？文[1]中提到，如果 $f$ 是凸函数且 $g \\in \\partial f(x)$ ，会有

同时** $f_{\\mu}(x)$ 和 $f(x)$ 之间的误差和函数 $f(x)$ 不同阶数的光滑性有关**，如下定理所示：

有趣的是， $f_{\\mu}(x)$ 比 $f(x)$ 具有更好的光滑性：

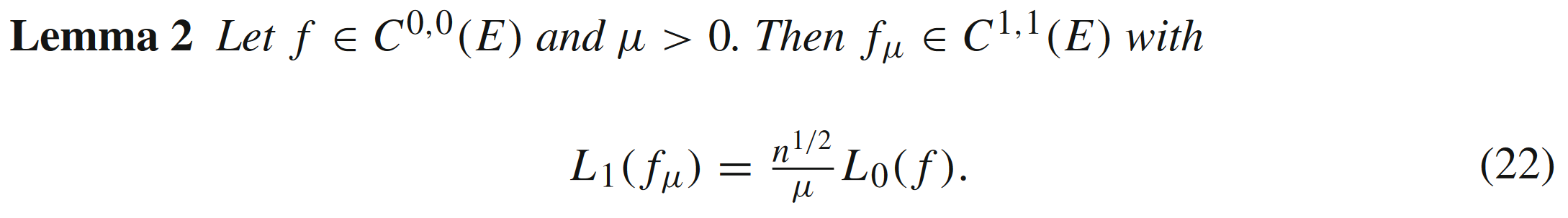
Lemma 2说明只要 $f(x)$ 连续， $f_{\\mu}(x)$ 永远都是可导函数。 (补充: 函数的可导性可以改善一阶算法收敛的算法复杂度，对非光滑函数进行光滑函数近似还有其他的方法，感兴趣的同学可以参看Nesterov的另外一篇文章[2]。)

其中， $\\partial_{\\epsilon}f(x)$ 被定义为

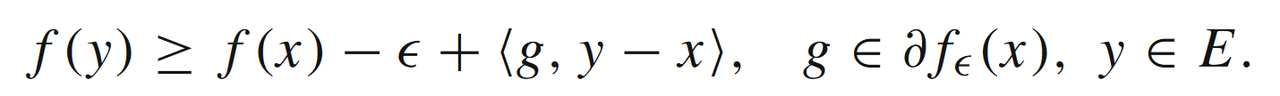
同样的，对于 $f_{\\mu}(x)$ 和 $f(x)$ 的梯度信息误差，也同样与函数的光滑性有关。如果 $f$ 有更高阶的光滑性，那么我们可以进一步得到有关高阶Lipschitz系数的误差分析：

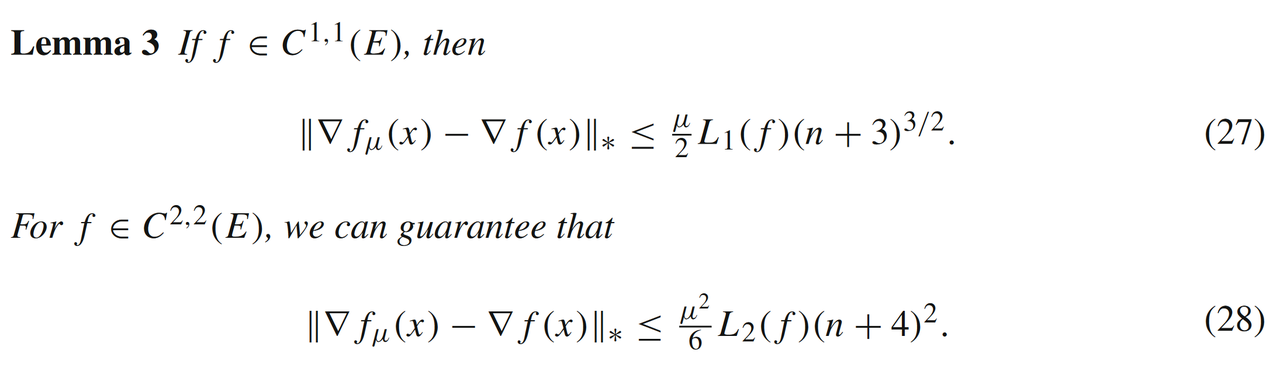
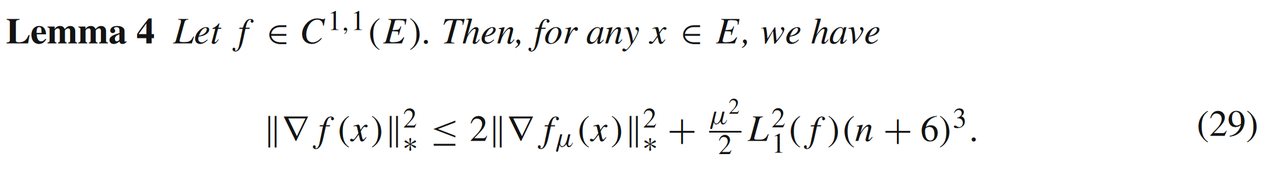
通过高斯近似函数 $f_{\\mu}$ 作为媒介，我们可以进一步分析随机梯度 $g_{\\mu}(x,u)$ 与原函数 $f(x)$ 梯度的关系。

在实际情况中， $\ abla f_{\\mu}(x)$ 本身是很难求得的，所以实际算法中（如算法（1））我们会使用 $\ abla f_{\\mu}(x)$ 的采样 $g_\\mu(x,u)$ 来进行计算。假设随机方向 $u$ 满足协方差矩阵为 $B^{-1}$ 的多维高斯分布，那我们有 $g_0(x,u), g_{\\mu}(x,u)$ 定义为

$g_0(x,u) :=f'(x, u) \\cdot Bu, \\\\$ $g_{\\mu}(x,u) :=\\frac{f(x+\\mu u)? f (x) }{\\mu}\\cdot Bu. \\\\$

文[1]还定义了 $\\hat{g}_{\\mu}(x,u)$

$\\hat{g}_{\\mu}(x,u) :=\\frac{f(x+\\mu u)? f (x- \\mu u) }{2\\mu}\\cdot Bu. \\\\$

对于上述三种梯度估计，文[1]提供了对应的上界估计：

从定理3和定理4可以看出， $g_0(x,u), g_{\\mu}(x,u), \\hat{g}_{\\mu}(x,u)$ 的二阶矩和原函数 $f$ 的梯度 $\ abla f(x)$ 有关，还和函数的光滑性有关( $C^{0,0}, C^{1,1}, C^{2,2}$ 得到不同的不等式)。同样的， $g_{\\mu}(x,u)$ 的二阶矩与 $f_{\\mu}(x)$ 存在类似的关系

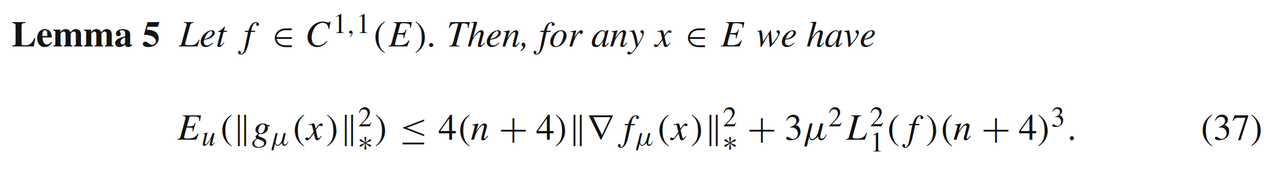
对于

$f^* :=\\min_{x \\in Q}f(x), \\\\$

如果函数 $f$ 本身是非光滑的，那么我们可以将 $g_{\\mu}(x,u)\\\\$ 当成随机梯度，那么算法（1）变为投影随机梯度法

$x_{k+1}=\\Pi_{Q}(x_k ? h_k B^{-1}g_{\\mu}(x,u)). \\qquad \\qquad \\\\$

对于序列 $\\{x_{k}\\}$ ，文[1]中给出了如下不等式：

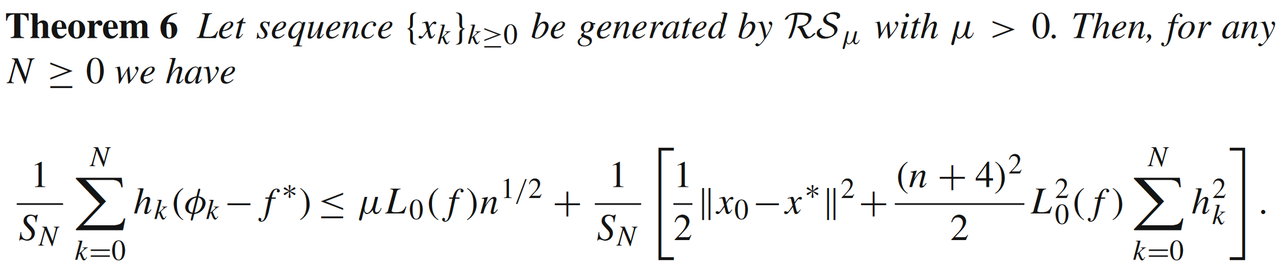
其中 $S_N=\\sum_{k=0}^{N}h_k$ ， $\\phi_k :=\\mathbf{E}_{u_{k-1}, ..., u_0}(f(x_k))$ 。如果熟悉一阶算法收敛性分析，可以发现，不等式右边多出了 $\\mu L_0 n^{1/2}$ 和 $\\sum_{k=0}^{N}h_k^2$ 两项。如果我们希望 $f(x_k)$ 有 $\\epsilon$ 最优，那么我们需要选取**合适的步长 $h_k$ 以及合适的高斯近似参数 $\\mu$ **：

当我们进一步放松条件，假设我们的问题变成一个随机优化问题，

$f^* :=\\min_{x \\in Q}f(x)=\\min_{x \\in Q}\\mathbb{E}_{\\zeta}[F(x,\\zeta)]. \\\\$

那么我们每次采样的函数值也带有随机误差，即 $F(x,\\zeta)$ 。同理，对应的随机梯度可以定义成

$s_0(x,\\zeta,u) :=D_x F(x, \\zeta,u)[u]\\cdot Bu, \\\\$ $s_{\\mu}(x,\\zeta,u) :=\\frac{F(x+\\mu u,\\zeta)? F(x,\\zeta) }{\\mu}\\cdot Bu. \\\\$ $\\hat{s}_{\\mu}(x,\\zeta,u) :=\\frac{F(x+\\mu u, \\zeta)? F(x- \\mu u, \\zeta) }{2\\mu}\\cdot Bu. \\\\$

对应的，算法（1）的变形为

$x_{k+1}=\\Pi_{Q}(x_k ? h_k B^{-1}s_{\\mu}(x,\\zeta,u)). \\qquad \\qquad \\\\$

可以看到，在这个随机优化算法中，有双层的随机影响，一层来源于问题本身的扰动， $\\zeta$ ，另一部分来源于我们采用的算法， $u$ 。同样的，通过合适选取步长 $h_k$ 和高斯近似参数 $\\mu$ ，我们可以得到 $O(n^2/\\epsilon^{2})$ 的收敛速率。

除了上述两种问题类型，文[1]中还介绍了其他三类问题：

$f$ 为一阶光滑函数
设计关于 $f$ 的加速算法
$f$ 为非凸优化问题

上述三种情况下的算法复杂度分析同样依赖于选取合适的步长 $h_k$ 和高斯近似参数 $\\mu$ ，最后的结果也与我们在一阶算法中的复杂度差不多。可能这个复杂度结果挺让人意外的，为什么零阶算法的复杂度会和一阶算法差不多？如果深入了解后可以发现，为了得到的相同的复杂度分析，我们需要将高斯近似参数 $\\mu$ 取得足够小才行，需要达到 $O(\\epsilon)$ 的数量级。此外，步长 $h_k$ 和高斯近似参数 $\\mu$ 的选取随着问题维度 $n$ 的增加要进一步变小。这就导致零阶算法的步长选取往往比一阶算法还需要小很多。因此最近几年有许多研究工作也是围绕着如何减小步长 $h_k$ 和高斯近似参数 $\\mu$ 对于维度 $n$ 的依赖展开的。

最后，想大致谈谈文[1]的零阶算法和传统的有限差分的区别。两者都是可以用来对原有问题梯度 $\ abla f(x)$ 进行估计。有限差分的梯度估计公式为

$g_{\ u}(x)=\\sum^{n}_{j=1}\\frac{f(x + \ u e_j ) ? f(x ? \ u e_j )}{2\ u}e_j. \\\\$

差分量 $\ u$ 的作用与高斯近似参数 $\\mu$ 是一样的。但是，梯度估计误差 $\\|g_{\ u}(x) - \ abla f(x)\\|$ 只会和 $\ u$ 和梯度的L-光滑性相关，

$\\|g_{\ u}(x) - \ abla f(x)\\| \\le L\\sqrt{n}\ u \\\\$

而文[1]中梯度估计误差 $\\|g_{\\mu}(x,u) - \ abla f(x)\\|$ 除了与 $\\mu$ 有关，还会与当前点的梯度值 $\ abla f(x)$ 有关，并且与问题维度 $n$ 也相关（感兴趣的同学可以研究文中定理4的推理）。

[1]Nesterov, Y., Spokoiny, V. Random Gradient-Free Minimization of Convex Functions. Found Comput Math 17, 527–566 (2017). https://doi.org/10.1007/s10208-015-9296-2

[2]Nesterov, Y. Smooth minimization of non-smooth functions. Math. Program. 103, 127–152 (2005). https://doi.org/10.1007/s10107-004-0552-5

返回列表

联系我们

地址：广东省广州市天河区88号
电话：400-123-4567
点击图标在线留言，我们会及时回复

Title 优化｜随机零阶优化算法分析

Title
优化｜随机零阶优化算法分析