Matlab优化方法

一、求无约束多变量（多元）极小值非线性优化问题有fminsearch和fminunc
fminsearch利用了单纯形法的原理
fminunc利用了拟牛顿法的原理
这两个函数都容易陷入局部优化，并且结果的正确与否还要取决 于初值点x0的选取。

1 fminsearch
[x,fval,exitflag,output] = fminsearch(…)
　　结构输出output，包含最优化函数的信息：output.algorithm 使用的优化算法，output.funcCount 函式计算（评价）次数，output.iterations 迭代次数，output.message 退出信息
　　exitflag值来表示fminsearch退出的条件：1–函数找到结果x，0–函数最大评价次数达到，或者是迭代次数达到（评价次数=迭代次数*参数个数），-1–算法由外部函数结束
　　fval:在结果x处的目标函数的函数值
　　x:解（可以为向量或者矩阵）

2 fminunc
[x,fval,exitflag,output,grad,hessian] = fminunc(… )
　　hessian:解x的海森（Hessian）矩阵

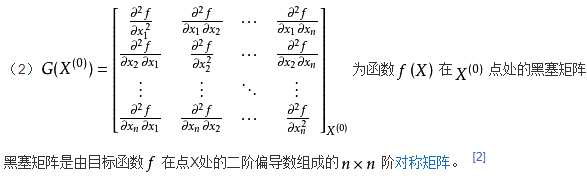
　　grad:解x处的梯度
　　exitflag:退出标志：大于0时表明函数收敛于x，等于0时表示达到最大迭代次数或者最大目标函数评价次数，小于0时表示函数不收敛
　　其他参数同上

fminunc为无约束优化提供了大型优化和中型优化算法。之前由options中的参数LargeScale控制：LargeScale='on’使用大型算法，LargeScale='off’使用中型算法。当前设置在‘Algorithm’。

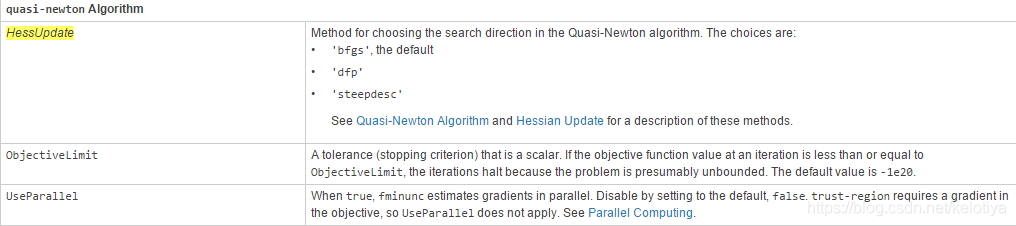
　　fminunc为中型优化算法的搜索方向提供了３种算法，由options中的参数HessUpdate控制：
　　HessUpdate=‘bfgs’（默认值），拟牛顿法的BFGS公式
　　HessUpdate=‘dfp’，拟牛顿法的DFP公式
　　HessUpdate=‘steepdesc’，最速下降法
　
　　fminunc为中型优化算法的步长一维搜索提供了两种算法，由options中参数LineSearchType控制：
　　LineSearchType=‘quadcubic’（缺省值），混合的二次和三次多项式插值
　　LineSearchType=‘cubicpoly’，三次多项式插值
　　
　　使用fminunc和fminsearch可能会得到局部最优解

二、求有约束多变量（多元）极小值非线性优化问题fmincon

[x,fval,exitflag]=fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)

返回值同上
输入值如下：
　　fun是用M文件定义的函数f(x),代表了(非)线性目标函数，
　　x0是x的初始值，
　　A,b,Aeq,beq定义了线性约束 ,如果没有线性约束，则A=[],b=[],Aeq=[],beq=[]，
　　lb和ub是变量x的下界和上界，如果下界和上界没有约束，则lb=[],ub=[],也可以写成lb的各分量都为 -inf,ub的各分量都为inf（多元变量这的lb与ub都为向量，每一个元素代表对每一个变量的约束），
　　nonlcon是用M文件定义的非线性向量函数约束，
　　options定义了优化参数，不填写表示使用Matlab默认的参数设置
　　
　　fmincon函数提供了大型优化算法和中型优化算法。默认时，若在fun函数中提供了梯度（options参数的GradObj设置为on），并且只有上下界存在或只有等式约束，fmincon函数将选择大型算法。当既有等式约束又有梯度约束时，使用中型算法。
　　fmincon函数的中型算法使用的是序列二次规划法。在每一步迭代中求解二次规划子问题，并用BFGS法更新拉格朗日Hessian矩阵。
　　fmincon函数可能会给出局部最优解，这与初值X0的选取有关。

三、控制参数options的设置
　　Options中常用的几个参数的名称、含义、取值如下:
(1) Display: 显示水平.取值为’off’时,不显示输出; 取值为’iter’时,显示每次迭代的信息;取值为’final’时,显示最终结果.默认值为’final’,notify只有当求解不收敛的时候才显示结果.
(2) MaxFunEvals: 允许进行函数评价的最大次数,取值为正整数.（评价次数=迭代次数*参数个数）
(3) MaxIter: 允许进行迭代的最大次数,取值为正整数
(4) TolFun：函数值（计算结果）精度，正整数。
(5) TolX：自变量的精度，正整数。
(6) Algorithm:使用的算法，如果函数能够提供梯度则选择"trust-region"选项，否则选择 拟牛顿法 -“quasi-newton”。

控制参数options可以通过函数optimset或者optimoptions创建或修改。命令的格式如下：
(1) options=optimset(‘optimfun’)
创建一个含有所有参数名,并与优化函数optimfun相关的默认值的选项结构options.
(2)options=optimset(‘param1’,value1,’param2’,value2,…)
创建一个名称为options的优化选项参数,其中指定的参数具有指定值,所有未指定的参数取默认值.
(3)options=optimset(oldops,‘param1’,value1,’param2’,value2,…)
创建名称为oldops的参数的拷贝,用指定的参数值修改oldops中相应的参数.
例：opts=optimset(‘Display’,’iter’,’TolFun’,1e-8)
该语句创建一个称为opts的优化选项结构,其中显示参数设为’iter’, TolFun参数设为1e-8.

四、问题结构模型
problem.options=options;
problem.x0=…;
problem.objective=@loss;(目标函数)
problem.sover=‘fminunc’;
[X,fval,exitflag]= fminunc(problem);

fmincon的如下：

五、优化函数通用参数




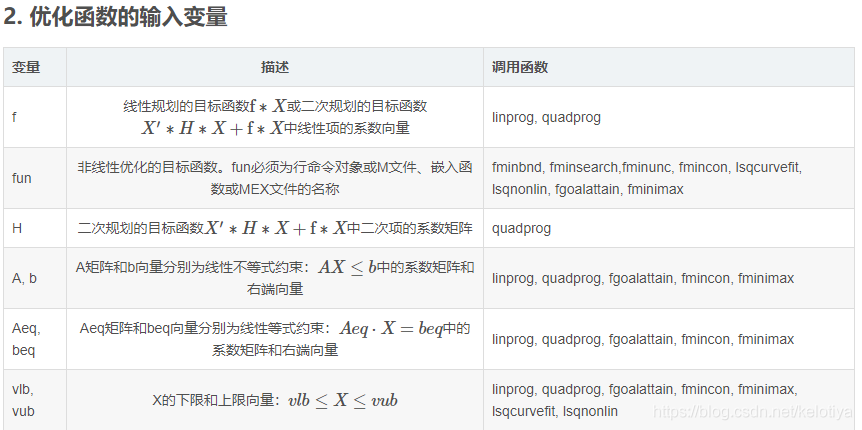
参考：
[1]https://blog.csdn.net/cclethe/article/details/77200997?utm_source=blogxgwz4
[2]https://blog.csdn.net/u013555719/article/details/97260571