本科毕业论文写路径优化，有哪些不涉及编程的研究方法？

Title
本科毕业论文写路径优化，有哪些不涉及编程的研究方法？

发布时间：2024-04-29 05:34:20 作者：佚名点击量：

本科，毕业论文是给定了一个具体城市，要求对其应急物流做路径优化，专业有学过编程，但是基本没用，想问一下路径优化有哪些不涉及算法的方法。

对于应急物流的路径优化问题，有一些方法可以帮助优化路径而不涉及复杂的算法。以下是一些不涉及算法的可能有用的方法：

了解地形：熟悉城市的地形、建筑物和道路系统可以帮助规划最优路径。考虑到交通流量、拥堵情况和道路状况等因素，可以优化物流的路径。
利用GPS技术：利用GPS技术可以精确定位物流车辆的位置，从而帮助规划最优路径。
使用交通管理系统：某些城市可能有交通管理系统，可以通过该系统了解道路的拥堵情况和交通状况，从而帮助规划最优路径。
运用物流管理软件：使用专业的物流管理软件可以帮助规划最优路径，并优化货物的运输和交付。
考虑配送区域和交通规划：考虑到城市的交通规划和区域划分，可以根据不同的配送区域规划物流路径。

以上方法都是可以通过技术手段实现的，不需要涉及太多的算法。同时，您还可以参考相关文献或向相关领域的专家咨询，了解更多路径优化的方法和技术

以下是一些关于应急物流路径优化方面的相关文献，您可以参考：

吴士波，张大伟，韩振宇，等. 基于混合遗传算法的物流配送路径优化[J]. 物流技术, 2021, 40(04): 147-151.
熊佳，黄鸣，谢凯. 基于改进遗传算法的城市应急物流路径优化[J]. 物流技术, 2020, 39(22): 147-150.
黄静慧，陈一鸣，刘颖. 基于模拟退火算法的应急物流路径优化[J]. 物流技术, 2019, 38(15): 147-150.
谢文龙，徐婧，吴晓巍. 城市应急物流路径规划及优化方法研究[J]. 物流技术, 2019, 38(19): 162-165.
郭磊，刘晓鹏，王倩. 基于动态规划的城市应急物流路径规划研究[J]. 物流技术, 2019, 38(22): 157-159.
胡文君，范卫华，王洪平. 基于模糊综合评判的应急物流路径优化模型[J]. 物流技术, 2018, 37(11): 157-160.
马少文，汤志辉，邱卫. 城市应急物流路径优化研究综述[J]. 物流技术, 2018, 37(20): 154-156.

以上文献可能涉及到一些算法方法，但仍可供您参考优化路径的方法和技术。另外，您还可以在学术搜索引擎（如Google Scholar、CNKI、万方等）上搜索相关论文以获取更多信息。

这些文献中的大多数都来自《物流技术》这个杂志，您可以前往该杂志的官方网站进行查询和下载。另外，一些文献也可以在一些学术搜索引擎上搜索和获取，如：

CNKI：https://www.cnki.net/
万方数据：http://www.wanfangdata.com.cn/index.html
Google Scholar：https://scholar.google.com/

在这些网站上，您可以通过关键词搜索相应的论文题目或作者来找到相关文献，并获取其链接或全文。希望这些信息可以帮助到您。

路径规划和跟踪控制算法是保障智能驾驶汽车在环境部分已知状态下实现安全行驶的核心因素，两者之间有着紧密的联系，规划路径的合理性与安全性及路径跟踪的精度是保证智能车辆安全行驶的关键所在。传统的路径规划和跟踪控制算法输出性能在实际驾驶场景中存在不同缺陷。同时，由于目前应用于路径规划及跟踪控制领域的多数算法最初的应用主体为移动机器人，所以在直接将其应用于车辆时也表现出了许多明显的不足，如对结构参数的考虑不足、运动学或动力学模型不匹配等。

路径规划和跟踪控制算法在智能驾驶研究中有重要意义，因此本文以校园环境中运行的智能车为研究对象，主要从智能驾驶汽车全局路径规划算法、局部路径规划算法和跟踪控制算法三个方面展开研究，具体的研究内容如下：

首先基于校园场景下结构化道路特征对环境进行建模，提出一种基于关键节点信息的改进 A*算法，并将其应用于全局路径规划环节中；通过地图预览、应用基于安全距离的碰撞场改进传统 A*算法代价函数、应用准均匀三次 B 样条曲线结合地图预览信息对路径进行有效平滑等方式，实现了 A*算法的计算效率、规划路径的安全性和可行性的综合提升。

其次，本文通过对经典局部路径规划算法动态窗口算法和向量场直方图算法进行对比，分析不同算法应用于局部道路环境下的综合表现，并最终选择了 DWA 算法用于智能驾驶车辆局部路径规划，对 DWA 算法进行了改进研究，改进 DWA 算法实时性和规划路径安全性都能够较好地满足车辆实际行驶需求。

再次，在路径跟踪控制方面，本文主要通过采用模型预测控制算法实现低速状态下对期望路径的准确跟踪。仿真结果表明，模型预测路径跟踪控制器能够在保持车辆稳定性的基础上，实现对期望路径的精确跟踪。其次，通过构建 Stanley 算法实现对期望速度的稳定跟踪。

%%%%%%%%%%%%%%%%%离散粒子群算法解决0-1背包问题%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%初始化%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clear all;              %清除所有变量
close all;              %清图
clc;                    %清屏
N=100;                  %群体粒子个数
D=10;                   %粒子维数
T=200;                  %最大迭代次数
c1=1.5;                 %学习因子1
c2=1.5;                 %学习因子2
Wmax=0.8;               %惯性权重最大值
Wmin=0.4;               %惯性权重最小值
Vmax=10;                %速度最大值
Vmin=-10;               %速度最小值
V=300;                             %背包容量
C=[95,75,23,73,50,22,6,57,89,98];  %物品体积
W=[89,59,19,43,100,72,44,16,7,64]; %物品价值
afa=2;                             %惩罚函数系数
%%%%%%%%%%%%%%%%初始化种群个体（限定位置和速度）%%%%%%%%%%%%%%%%
x=randint(N,D);        %随机获得二进制编码的初始种群
v=rand(N,D) * (Vmax-Vmin)+Vmin;
%%%%%%%%%%%%%%%%%%初始化个体最优位置和最优值%%%%%%%%%%%%%%%%%%%
p=x;
pbest=ones(N,1);
for i=1:N
    pbest(i)=func4(x(i,:),C,W,V,afa);
end
%%%%%%%%%%%%%%%%%%%初始化全局最优位置和最优值%%%%%%%%%%%%%%%%%%
g=ones(1,D);
gbest=eps;
for i=1:N
    if(pbest(i)>gbest)
        g=p(i,:);
        gbest=pbest(i);
    end
end
gb=ones(1,T);
%%%%%%%%%%%按照公式依次迭代直到满足精度或者迭代次数%%%%%%%%%%%%%
for i=1:T
    for j=1:N
        %%%%%%%%%%%%%%更新个体最优位置和最优值%%%%%%%%%%%%%%%%%
        if (func4(x(j,:),C,W,V,afa)>pbest(j))
            p(j,:)=x(j,:);
            pbest(j)=func4(x(j,:),C,W,V,afa);
        end
        %%%%%%%%%%%%%%%%更新全局最优位置和最优值%%%%%%%%%%%%%%%
        if(pbest(j)>gbest)
            g=p(j,:);
            gbest=pbest(j);
        end
        %%%%%%%%%%%%%%%%计算动态惯性权重值%%%%%%%%%%%%%%%%%%%%
        w=Wmax-(Wmax-Wmin)*i/T;
        %%%%%%%%%%%%%%%%%跟新位置和速度值%%%%%%%%%%%%%%%%%%%%%
        v(j,:)=w*v(j,:)+c1*rand*(p(j,:)-x(j,:))...
            +c2*rand*(g-x(j,:));
        %%%%%%%%%%%%%%%%%%%%边界条件处理%%%%%%%%%%%%%%%%%%%%%%
        for ii=1:D
            if (v(j,ii)>Vmax)  |  (v(j,ii)< Vmin)
                v(j,ii)=rand * (Vmax-Vmin)+Vmin;
            end
        end    
        vx(j,:)=1https://www.zhihu.com/question/(1+exp(-v(j,:)));
        for jj=1:D
            if vx(j,jj)>rand
                x(j,jj)=1;
            else
                x(j,jj)=0;
            end
        end      
    end
    %%%%%%%%%%%%%%%%%%%%记录历代全局最优值%%%%%%%%%%%%%%%%%%%%%
    gb(i)=gbest;
end
g;                       %最优个体 
figure
plot(gb)
xlabel('迭代次数');
ylabel('适应度值');
title('适应度进化曲线')

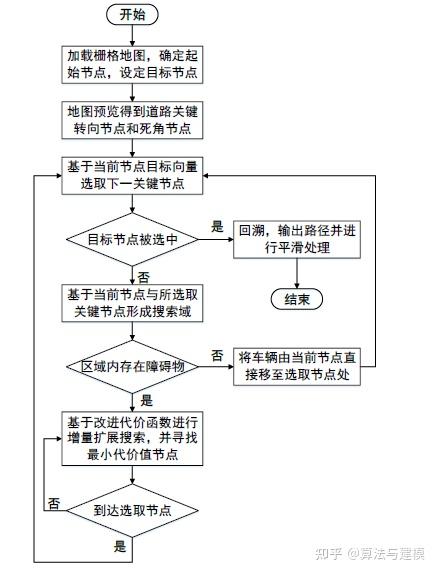
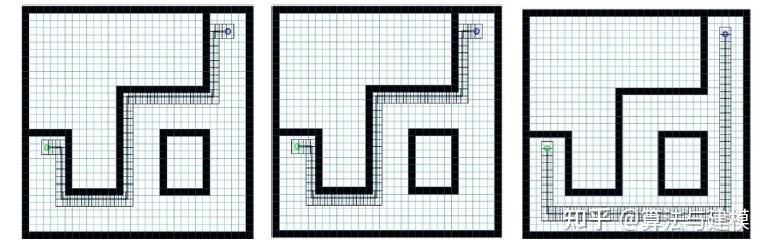
基于地图预览模块获取的道路转向关键节点和在行驶过程中产生的避障转向节点进行路径平滑，采用准均匀三次 B 样条曲线对相应的轨迹进行优化。如图 2-10 为不同形式路径的平滑示意图。如图 2-10 分别为基于道路转向关键节点和避障转向节点进行的路径平滑过程示意图。其中，基于道路转向关键节点进行路径平滑时，共选用 7个控制节点，其位置分别为基于选定的关键转向节点向两侧各扩展相等间距为 1m 的三个节点；基于避障转向节点进行平滑时，以两个变向节点为主要控制点，向前后两侧扩展相等间距为 1m 的三个节点得到另外六个补充控制点。

蜣螂优化算法（Dung beetle optimizer，DBO）由Jiankai Xue和Bo Shen于2022年提出，该算法主要受蜣螂的滚球、跳舞、觅食、偷窃和繁殖行为的启发所得。https://blog.csdn.net/weixin_46204734/article/details/128138381

参考文献：Xue, J., Shen, B. Dung beetle optimizer: a new meta-heuristic algorithm for global optimization. J Supercomput (2022). https://doi.org/10.1007/s11227-022-04959-6

狐猴优化算法（Lemurs Optimizer，LO）由Ammar Kamal Abasi等人于2022年提出，该算法模拟狐猴的跳跃和跳舞行为，具有结构简单，思路新颖，搜索速度快等优势。https://blog.csdn.net/weixin_46204734/article/details/133391050

参考文献：

[1]Abasi AK, Makhadmeh SN, Al-Betar MA, Alomari OA, Awadallah MA, Alyasseri ZAA, Doush IA, Elnagar A, Alkhammash EH, Hadjouni M. Lemurs Optimizer: A New Metaheuristic Algorithm for Global Optimization. Applied Sciences. 2022; 12(19):10057. Applied Sciences | Free Full-Text | Lemurs Optimizer: A New Metaheuristic Algorithm for Global Optimization

蜘蛛蜂优化算法（Spider wasp optimizer，SWO）由Mohamed Abdel-Basset等人于2023年提出，该算法模型雌性蜘蛛蜂的狩猎、筑巢和交配行为，具有搜索速度快，求解精度高的优势。https://blog.csdn.net/weixin_46204734/article/details/133999858

参考文献：

[1]Abdel-Basset, M., Mohamed, R., Jameel, M. et al. Spider wasp optimizer: a novel meta-heuristic optimization algorithm. Artif Intell Rev (2023). Spider wasp optimizer: a novel meta-heuristic optimization algorithm | SpringerLink

小龙虾优化算法（Crayfsh optimization algorithm，COA）由Jia Heming 等人于2023年提出，该算法模拟小龙虾的避暑、竞争和觅食行为，具有搜索速度快，搜索能力强，能够有效平衡全局搜索和局部搜索的能力。https://blog.csdn.net/weixin_46204734/article/details/132939275

参考文献：

[1]Jia, H., Rao, H., Wen, C. et al. Crayfish optimization algorithm. Artif Intell Rev (2023). Crayfish optimization algorithm | SpringerLink

光谱优化算法（Light Spectrum Optimizer，LSO）由Mohamed Abdel-Basset等人于2022年提出。https://blog.csdn.net/weixin_46204734/article/details/132221896

参考文献：

[1]Abdel-Basset M, Mohamed R, Sallam KM, Chakrabortty RK. Light Spectrum Optimizer: A Novel Physics-Inspired Metaheuristic Optimization Algorithm. Mathematics. 2022; 10(19):3466. Mathematics | Free Full-Text | Light Spectrum Optimizer: A Novel Physics-Inspired Metaheuristic Optimization Algorithm

开普勒优化算法（Kepler optimization algorithm，KOA）由Mohamed Abdel-Basset等人于2023年提出。https://blog.csdn.net/weixin_46204734/article/details/131743115

参考文献：

Mohamed Abdel-Basset, Reda Mohamed, Shaimaa A. Abdel Azeem, Mohammed Jameel, Mohamed Abouhawwash, Kepler optimization algorithm: A new metaheuristic algorithm inspired by Kepler’s laws of planetary motion, Knowledge-Based Systems, 2023. DOI: Redirecting

淘金优化算法（Gold rush optimizer，GRO）由Kamran Zolf于2023年提出，其灵感来自淘金热，模拟淘金者进行黄金勘探行为。https://blog.csdn.net/weixin_46204734/article/details/134023570

参考文献：

K. Zolfi. Gold rush optimizer: A new population-based metaheuristic algorithm. Operations Research and Decisions 2023: 33(1), 113-150. DOI 10.37190/ord230108

单个无人机三维路径规划问题及其建模_IT猿手的博客-CSDN博客

参考文献：

[1]胡观凯,钟建华,李永正,黎万洪.基于IPSO-GA算法的无人机三维路径规划[J].现代电子技术,2023,46(07):115-120

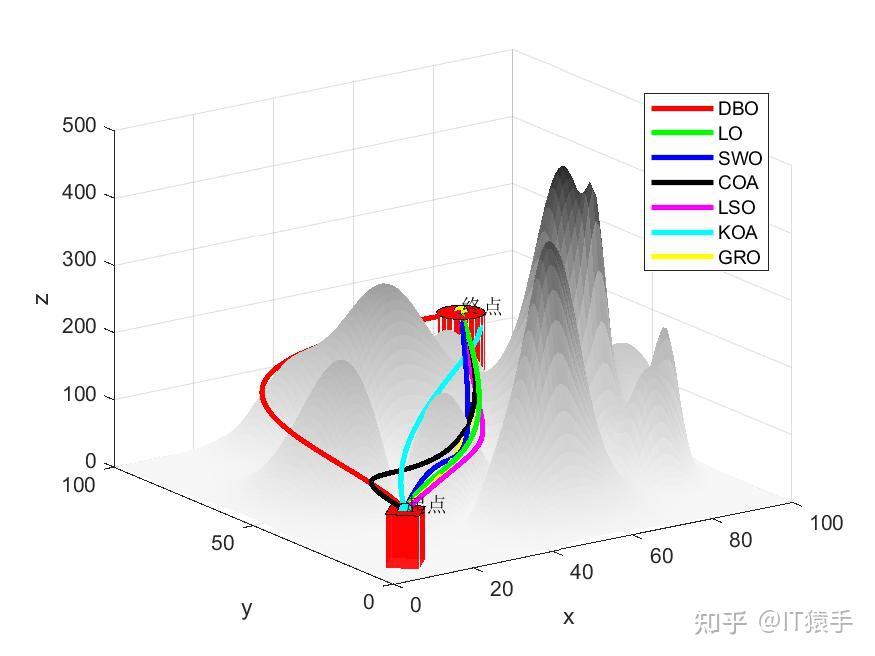
无人机航迹规划MATLAB：七种优化算法（DBO、LO、SWO、COA、LSO、KOA、GRO）求解无人机路径规划-CSDN博客

（1）部分代码

close all
clear  
clc
、warning off;
%% 三维路径规划模型定义
global startPos goalPos N
N=2;%待优化点的个数(可以修改)
startPos=[10, 10, 80]; %起点(可以修改)
goalPos=[80, 90, 150]; %终点(可以修改)
SearchAgents_no=30; % 种群大小(可以修改)
Function_name='F1'; %F1:随机产生地图 F2：导入固定地图
Max_iteration=100; %最大迭代次数(可以修改)
% Load details of the selected benchmark function
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);
AlgorithmName={'DBO','LO','SWO','COA','LSO','KOA','GRO'};%算法名称
addpath('https://www.zhihu.com/question/AlgorithmCode/')%添加算法路径
bestFit=[];%保存各算法的最优适应度值
for i=1:size(AlgorithmName,2)%遍历每个算法，依次求解当前问题
Algorithm=str2func(AlgorithmName{i});%获取当前算法名称，并将字符转换为函数
[Best_score,Best_pos,Convergence_curve]=Algorithm(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);%当前算法求解
%将当前算法求解结果放入data中
data(i).Best_score=Best_score;%保存该算法的Best_score到data
data(i).Best_pos=Best_pos;%保存该算法的Best_pos到data
data(i).Convergence_curve=Convergence_curve;%保存该算法的Convergence_curve到data
bestFit=[bestFit data(i).Best_score];
end

%%  画各算法的直方图
figure 
bar(bestFit)
ylabel('无人机飞行路径长度');
set(gca,'xtick',1:1:size(AlgorithmName,2));
set(gca,'XTickLabel',AlgorithmName)
saveas(gcf,'https://www.zhihu.com/question/Picture/直方图.jpg') %将图片保存到Picture文件夹下面


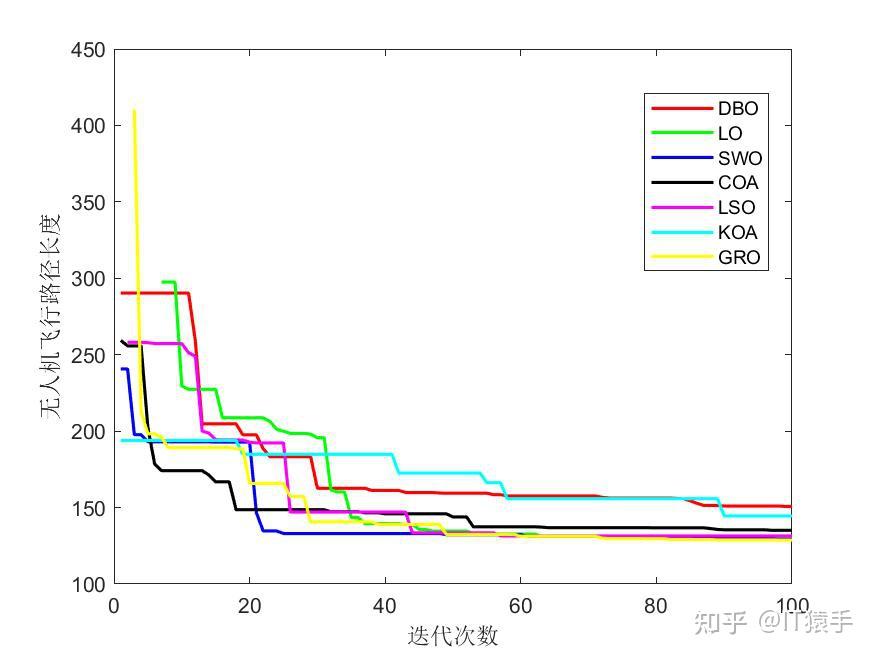
%%  画收敛曲线
strColor={'r-','g-','b-','k-','m-','c-','y-'};
figure
for i=1:size(data,2)
plot(data(i).Convergence_curve,strColor{i},'linewidth',1.5)%semilogy
hold on
end
xlabel('迭代次数');
ylabel('无人机飞行路径长度');
legend(AlgorithmName,'Location','Best')
saveas(gcf,'https://www.zhihu.com/question/Picture/收敛曲线.jpg') %将图片保存到Picture文件夹下面


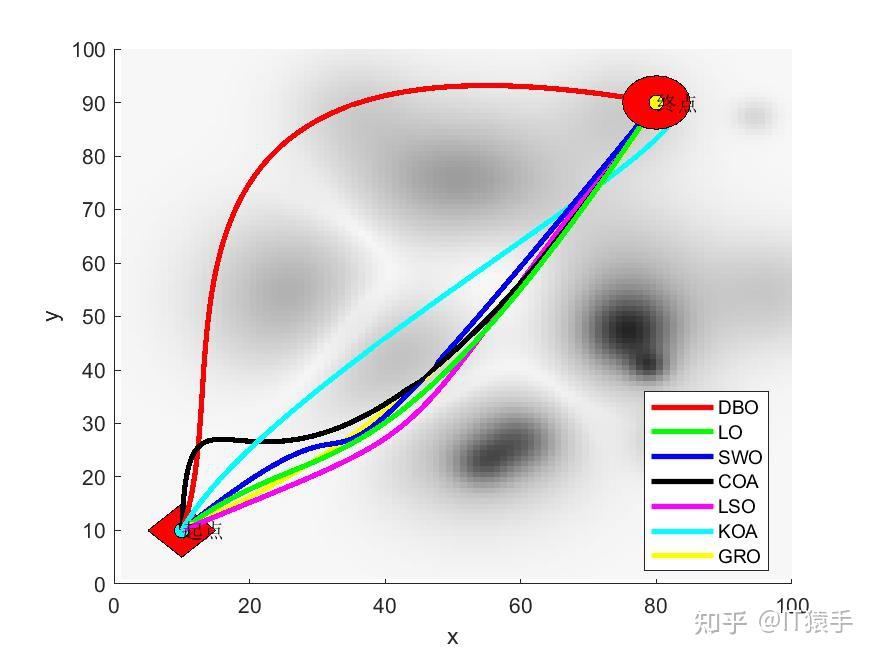
%% 显示三维图并保存
path=plotFigure(data,AlgorithmName,strColor);%path是各算法求解的无人机路径
saveas(gcf,'https://www.zhihu.com/question/Picture/路径曲线（三维）.jpg') %将图片保存到Picture文件夹下面


%% 显示二维图并保存
view(2)
saveas(gcf,'https://www.zhihu.com/question/Picture/路径曲线（二维）.jpg') %将图片保存到Picture文件夹下面

（2）部分结果

返回列表

联系我们

地址：广东省广州市天河区88号
电话：400-123-4567
点击图标在线留言，我们会及时回复

Title 本科毕业论文写路径优化，有哪些不涉及编程的研究方法？

Title
本科毕业论文写路径优化，有哪些不涉及编程的研究方法？